一、正排
当在投广告的总数较少(几百~几千)时,最简单的做法是遍历。但是如果广告数目太多,则时间复杂度太高O(n*m)
def ad_targeting(request, ads):
candidates = []
for ad in ads:
match = True
for field, value in request.tags:
if !ads.match(field, value):
match = False
break
if match:
candidates.append(ad)
return candidates二、倒排
构建倒排索引:
field_names = ["city", "gender", "age"]
def build_inverted_index(ads):
index = {} # field -> value -> array_of_ads
for ad in ads:
index["all"][NOT_SPECIFIED].add(ad)
for field in field_names:
value = ad.get_targeting_value(field)
if value is None:
index[field][NOT_SPECIFIED].add(ad)
else:
index[field][value].add(ad) # set.add
return index需要注意的细节:value 为 None 的情况,代表广告未设置该定向条件(例如不限性别),需要将该广告加入一个特定的集合里(value = NOT_SPECIFIED)。
然后在收到流量请求时,将每个定向条件的倒排集合求交,即可得到所有可投的广告:
def ad_targeting(request, index):
ads = None
for field in field_name:
value = request.tags.get(field)
if value is None:
# 流量缺失该标签,只能投放未定向该标签的广告
field_ads = index["field"][NOT_SPECIFIED]
else:
# 可投放 [未定向该字段] 或 [定向该字段=某值]的广告
field_ads = copy(index["field"][NOT_SPECIFIED])
field_ads.union(index["field"][value])
if ads is None:
ads = field_ads
else:
ads.intersect(field_ads)
return ads具体实现还可以有一些改进点:
1.在同一个定向条件下可以选择多个取值,例如希望投放一线城市,那么就应该是 city in [北、上、广、深];
2.定向条件可能还需要支持取反,例如 city not in [北、上、广、深],可以用集合求差集来实现;
3.对于年龄等取值较多的字段,可以采用划分年龄段的方式减少倒排的枚举值。
三、bitmap
bitmap结构一般作为倒排key value中的value,代表的是当前key条件下的广告集合。
通过引入 bitmap ,我们可以大幅提高集合操作(交、并、差)的运算效率:由于数据是连续存储且位运算不需要比较操作,因此能显著提高 cache 命中率(包括数据 cache 和指令 cache )。
1.普通的bitmap
算法原理
当数据表中某个字段下取值范围较少时,比如对于性别,可取值的范围只有{‘男’,’女’},并且男和女可能各占该表的50%的数据,这时添加B树索引还是需要取出一半的数据查询。
如果用户查询的列的基数非常的小, 即只有的几个固定值,如性别、婚姻状况、行政区等等。要为这些基数值比较小的列建索引,就需要建立位图索引。
对于性别这个列,位图索引形成两个向量,男向量为10100…,(向量长度为N),向量的每一位表示该行是否是男,如果是则位1,否为0,同理,女向量位01011…。
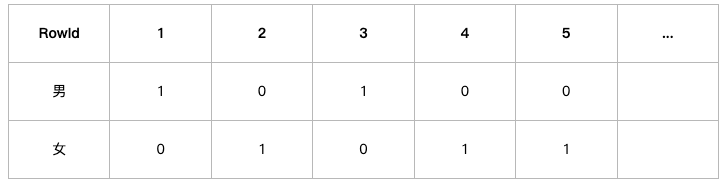
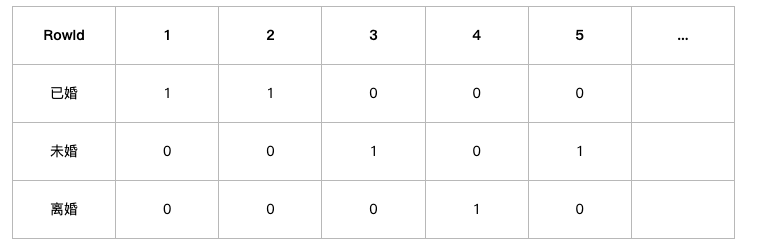
对于婚姻状况这一列,位图索引生成三个向量,已婚为11000…,未婚为00100…,离婚为00010…。
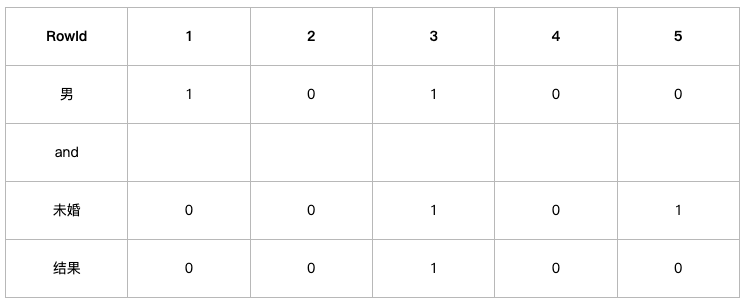
当我们使用查询语句“select * from table where Gender=‘男’ and Marital=“未婚”;”的时候 首先取出男向量10100…,然后取出未婚向量00100…,将两个向量做and操作,这时生成新向量00100…,可以发现第三位为1,表示该表的第三行数据就是我们需要查询的结果。
位图索引的适用条件
位图索引适合只有几个固定值的列,如性别、婚姻状况、行政区等等,而身份证号这种类型不适合用位图索引
此外,位图索引适合静态数据,而不适合索引频繁更新的列。举个例子,有这样一个字段busy,记录各个机器的繁忙与否,当机器忙碌时,busy为1,当机器不忙碌时,busy为0。
参考:https://www.cnblogs.com/lbser/p/3322630.html
2.压缩的bitmap(Roaring Bitmaps)
Bitmap 比较适用于数据分布比较稠密的存储场景中,对于原始的 Bitmap 来说,若要存储一个 uint32 类型数据(在广告的场景中就是指广告数量有2^32个),这就需要 2 ^ 32 长度的 bit 数组,通过计算可以发现(2 ^ 32 / 8 bytes = 512MB),一个普通的 Bitmap 需要耗费 512MB 的存储空间。如果我们只存储几个数据的话依然需要占用 512M 的话,就有些浪费空间了,因此我们可以采用对位图进行压缩的 RoaingBitmap,以此减少内存和提高效率。
算法原理
虽然位图索引可以显著加快查询速度,但是,位图索引会占用大量的内存,因此我们会更喜欢压缩位图索引。
RBM 的主要思想并不复杂,简单来讲,有如下三条:
我们将 32-bit 的范围 ([0, n)) 划分为 2^16 个桶,每一个桶有一个 Container 来存放一个数值的低16位;
在存储和查询数值的时候,我们将一个数值 k 划分为高 16 位(k % 2^16)和低 16 位(k mod 2^16),取高 16 位找到对应的桶,然后在低 16 位存放在相应的 Container 中;
容器的话, RBM 使用两种容器结构: Array Container 和 Bitmap Container。Array Container 存放稀疏的数据,Bitmap Container 存放稠密的数据。即,若一个 Container 里面的 Integer 数量小于 4096,就用 Short 类型的有序数组来存储值。若大于 4096,就用 Bitmap 来存储值。
举例说明
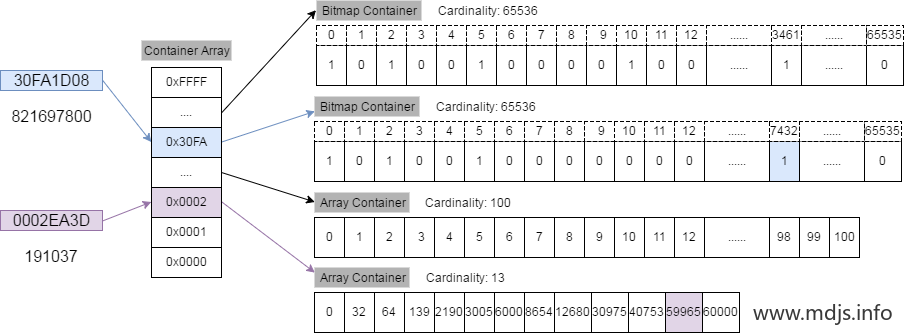
现在我们要将 821697800 这个 32 bit 的整数插入 RBM 中,整个算法流程是这样的:
821697800 对应的 16 进制数为 30FA1D08, 其中高 16 位为 30FA, 低16位为 1D08。
我们先用二分查找从一级索引(即 Container Array)中找到数值为 30FA 的容器(如果该容器不存在,则新建一个),从图中我们可以看到,该容器是一个 Bitmap 容器。
找到了相应的容器后,看一下低 16 位的数值 1D08,它相当于是 7432,因此在 Bitmap 中找到相应的位置,将其置为 1 即可。
原理补充
RBM 的基本原理就这些,基于这种设计原理会有一些额外的操作要提一下。
请注意上文提到的一句话:
若一个 Container 里面的 Integer 数量小于 4096,就用 Short 类型的有序数组来存储值。若大于 4096,就用 Bitmap 来存储值。
先解释一下为什么这里用的 4096 这个阈值?因为一个 Integer 的低 16 位是 2Byte,因此对应到 Arrary Container 中的话就是 2Byte * 4096 = 8KB;同样,对于 Bitmap Container 来讲,2^16 个 bit 也相当于是 8KB。
然后,基于前面提到的两种 Container,在两个 Container 之间的 Union (bitwise OR) 或者 Intersection (bitwise AND) 操作又会出现下面三种场景:
Bitmap vs Bitmap
Bitmap vs Array
Array vs Array
参考:
https://www.modb.pro/db/218968
(bitmap的缺点是反定向不太好做)
四、布尔索引
https://zhuanlan.zhihu.com/p/591048449
oppo的实践:https://blog.csdn.net/qianshangding0708/article/details/132372577
术语:
1.Attribute:单个流量标签,包含两个信息:属性类别和属性取值。如:AGE: 5
2.Assignment:多个流量标签组成的用户画像。如:AGE: 5,GENDER: 1,NETWORK: 1
3.Conjunction:布尔表达式的合取范式。如:AGE ∈ (4,5,6) ∧ GENDER ∈ (1)
两层索引设计的主要思想是:从Assignment 找出包含这些流量标签的Conjunction,筛选满足条件的Conjunction,根据筛选出的Conjunction,找出满足条件的广告集合。下面我们举个例子:
假设线上有7个广告,它们定向条件如下,其中A3和Ad7定向条件相同。Ad6包含反向定向,即该广告不能出在AppInterest的标签为(19-1)的用户上面。
Ad1定向:PlacementType∈(2)
Ad2定向:PlacementType∈(2) ∧ AppInterest∈(15-0, 19-1) ∧ InstalledApp∈(30202)
Ad3定向:PlacementType∈(2) ∧ AppInterest∈(15-0, 19-1) ∧ NetworkType∈(1)
Ad4定向:PlacementType∈(2) ∧ AppInterest∈(19-1)
Ad5定向:PlacementType∈(2) ∧ InstalledApp∈(30202) ∧ NetworkType∈(1)
Ad6定向:PlacementType∈(2) ∧ IpGeo∈(141) ∧ NetworkType∈(1) ∧ AppInterest∉(19-1)
Ad7定向:PlacementType∈(2) ∧ AppInterest∈(15-0, 19-1) ∧ NetworkType∈(1)对应定向条件有6个Conjuntion,可编号Conjuntion如下:
| conjunctionId | conjunction | size |
|---|---|---|
| 1 | PlacementType∈(2) | 1 |
| 2 | PlacementType∈(2) ∧ AppInterest∈(19-1) | 2 |
| 3 | PlacementType∈(2) ∧ IpGeo∈(141) ∧ NetworkType∈(1) ∧ AppInterest∉(19-1) | 3 |
| 4 | PlacementType∈(2) ∧ InstalledApp∈(30202) ∧ NetworkType∈(1) | 3 |
| 5 | PlacementType∈(2) ∧ AppInterest∈(15-0, 19-1) ∧ InstalledApp∈(30202) | 3 |
| 6 | PlacementType∈(2) ∧ AppInterest∈(15-0, 19-1) ∧ NetworkType∈(1) | 3 |
其中,conjunctionId为编号,conjunction为布尔表达式内容,size为∈语句的个数。
可以建立conjunctionId到Ad的索引如下:
conjunction1 -> Ad1
conjunction2 -> Ad4
conjunction3 -> Ad6
conjunction4 -> Ad5
conjunction5 -> Ad2
conjunction6 -> Ad3,Ad7流量标签到布尔表达式的索引如下:
| K | Attribute(Key) | PostingList(conjunctionId,代表包含/不包含) |
|---|---|---|
| 1 | PlacementType:2 | (1, ∈) |
| 2 | PlacementType:2 | (2, ∈) |
| AppInterest: 19-1 | (2, ∈) | |
| 3 | PlacementType:2 | (3, ∈), (4, ∈), (5, ∈), (6, ∈) |
| AppInterest:19-1 | (3, ∉), (5, ∈), (6, ∈) | |
| AppInterest:15-0 | (5, ∈), (6, ∈) | |
| InstalledApp:30202 | (4 ∈), (5, ∈) | |
| NetworkType: 1 | (3, ∈), (4, ∈), (6, ∈) | |
| IpGeo:141 | (3, ∈) |
如上图,建立K-Index
K 代表Conjuntion的size大小
PostingList代表包含/不包含这个Attribute的Conjuntion
算法原理
我们还是按照上面的例子说明,最后给出核心算法的伪代码。现在来了一个用户画像Assignment:
PlacementType:2
AppInterest:19-1
NetworkType:1由于有三个流量标签,那么我们满足条件的只可能是1-Index, 2-Index,3-Index。这就是为什么上面建索引的时候需要建立一个K-Index的索引,加上K-Index可以根据数目进行算法剪枝。同时每一个PostingList中的Conjuntion都已按照ConjuntionId升序排列。我们以检测3-Index为例。根据Assignment可以从索引里面取到如Conjuntions:
PlacementType: 2 (3, ∈), (4, ∈), (5, ∈), (6, ∈)
AppInterest: 19-1 (3, ∉), (5, ∈), (6, ∈)
NetworkType: 1 (3, ∈), (4, ∈), (6, ∈)需要判断当前最小的ConjuntionId至少出现在3个PostingList中,且不能出现∉的关系。
每次check完成之后按照conjuntionId重排序(方便检测是不是至少出现在3个PostingList中)。
PlacementType: 2 (3, ∈), (4, ∈), (5, ∈), (6, ∈)
AppInterest: 19-1 (3, ∉), (5, ∈), (6, ∈)
NetworkType: 1 (3, ∈), (4, ∈), (6, ∈)
\-------------------------------------------------------
MatchedConjuntion = []
(check Conjuntion3,发现出现了∉,故不满足)
PlacementType: 2 (4, ∈), (5, ∈), (6, ∈)
NetworkType: 1 (4, ∈), (6, ∈)
AppInterest: 19-1 (5, ∈), (6, ∈)
\-------------------------------------------------------
MatchedConjuntion = []
(check Conjuntion4,发现出现只出现在两个中,故不满足)
PlacementType: 2 (5, ∈), (6, ∈)
AppInterest: 19-1 (5, ∈), (6, ∈)
NetworkType: 1 (6, ∈)
\-------------------------------------------------------
MatchedConjuntion = []
(check Conjuntion5,发现出现只出现在两个中,故不满足)
PlacementType: 2 (6, ∈)
AppInterest: 19-1 (6, ∈)
NetworkType: 1 (6, ∈)
\-------------------------------------------------------
MatchedConjuntion = []
(check Conjuntion6,至少出现在三个中,且没有∉关系,满足)按照该算法继续检测2-Index、1-Index。得到最终结果: MatchedConjuntion =[1,2,6]。再根据MatchedConjuntion 检索出广告 MatchedAds = [Ad1, Ad4, Ad3,Ad7]。
维度爆炸问题
有的同学觉得这里会出现维度爆炸的问题,比如有50个兴趣标签,5个年龄段标签,2个性格标签。最极端的情况是可能会出现:
50 * 5 * 2 * ... = 100 * ...随着定向维度的增加而爆炸,实际上并不会,因为定向维度是取决于广告的规模的,最极端情况,假设我们线上有100w的广告,且这100w的广告定向标签都不一样,那么问题规模也是100w,并不会出现维度爆炸。另外,实际上,线上大量广告的定向标签是重复的,100w的广告定向的Conjuntion,远远小于广告数量。
基于DNF(析取范式)的布尔索引算法,伪代码
1: input: inverted list idx and assignment S
2: output: set of IDs O matching S
3: O ← ∅
/*
输入:预构建的分层倒排索引 idx和用户的属性集合 S。
输出:所有满足 S的合取子句ID的集合 O。
初始化:将存放结果的集合 O初始化为空。
*/
4: for K=min(idx.MaxConjunctionSize, |S|). . .0 do
/*
开始一个循环,变量K从(最大合取子句大小, 用户属性数S)中的较小者开始,递减到0。
原因:如果一个合取子句的K值(所需=断言的数量)大于用户提供的属性数|S|,那么它绝对不可能被满足。此循环确保了只检查可能被满足的K层。
*/
5: /* List of posting lists matching A for conjunction size K */
6: PLists ← idx.GetPostingLists(S,K)
/*
获取当前K值层中,所有与用户属性集S相关的Posting List。
例如,用户属性S有{age=18, city=北京, gender=男},K=2,那么这一步可能会获取到(age,18), (city,北京), (gender,男)这些Key在K=2层对应的Posting List。
*/
7: InitializeCurrentEntries(PLists)
8: /* Processing K=0 and K=1 are identical */
9: if K=0 then K ← 1
/*
初始化每个Posting List的指针,指向其第一个条目(Entry)。
处理K=0(合取子句中没有任何=断言,只有!=断言)和处理K=1在逻辑上是相似的,这里将K=0的情况统一转换为K=1来处理,简化后续代码
*/
10: /* Too few posting lists for any conjunction to be satisfied */
11: if PLists.size() < K then
12: continue to next for loop iteration
/*
剪枝优化:如果获取到的Posting List数量小于当前K值,说明没有任何合取子句能被满足。
原因:一个合取子句要被满足,需要满足其所有=断言。如果用户属性提供的(属性,值)对都无法覆盖K个=断言,那么这一层所有的合取子句都不可能被满足,直接跳过。
*/
13: while PLists[K-1].CurrEntry ≠ EOL do
/*
开始一个循环,只要第K个Posting List(数组从0开始,所以索引是K-1)的当前条目不是结束标志(End Of List),就继续循环。
选择第K个List作为基准是因为算法需要确保至少有K个List包含同一个Cid的候选。
*/
14: SortByCurrentEntries(PLists)
/*
重排序:根据所有Posting List当前指针所指条目的Cid重新排序List。排序规则通常是Cid升序,相同Cid时!=在前(反定向在前),=在后。
这一步是为了让所有List的当前条目有序,便于比较和跳跃。
*/
15: /* Check if the first K posting lists have the same conjunc-
tion ID in their current entries */
16: if PLists[0].CurrEntry.ID = PLists[K-1].CurrEntry.ID
then
/*
关键检查:如果第一个List的当前条目Cid和第K个List的当前条目Cid相同,这意味着前K个List的当前条目都指向同一个合取子句ID(因为列表是有序的,PLists[0]的Cid最小,PLists[K-1]的Cid最大,它们相等意味着中间所有List的当前Cid也必然等于这个值)。
这个Cid(记为X)就是一个候选ID,它可能是一个满足条件的合取子句。
*/
17: /* Reject conjunction if a ≠ predicate is violated */
18: if PLists[0].CurrEntry.AnnotatedBy(≠) then
/*
检查这个候选合取子句X是否因为!=断言而被拒绝。(反定向检查)
判断方法:因为排序时!=操作符的条目会排在=前面,如果第一个条目的操作符是!=,说明对于这个属性-值对,合取子句X的要求是“不等于”,但用户提供的恰好是“等于”,这违反了合取子句X的约束条件。
*/
19: RejectID ← PLists[0].CurrEntry.ID
20: for L = K .. (PLists.size()-1) do
21: if PLists[L].CurrEntry.ID = RejectID then
22: /* Skip to smallest ID where ID > RejectID */
23: PLists[L].SkipTo(RejectID+1)
24: else
25: break out of for loop
26: continue to next while loop iteration
/*
如果发现违反!=约束,则拒绝该候选ID(X)。
并且,跳过所有其他Posting List中当前条目也是X的情况,让它们的指针直接跳到X+1的位置。这是一个重要的性能优化,避免在明知不满足条件的情况下继续检查X。
随后,直接继续下一次while循环,检查下一个候选。
*/
27: else /*conjunction is fully satisfied */
28: O ← O ∪ {PLists[K-1].CurrEntry.ID}
/*
如果第一个条目的操作符是=,那么恭喜!这意味着合取子句X的所有=断言都被用户属性满足(因为我们有K个List指向X,且操作符都是=),并且没有!=断言被违反(因为如果违反,会在前面的if条件中被捕获)。因此,将合取子句ID X加入结果集 O。
*/
29: /* NextID is the smallest possible ID after current ID*/
30: NextID ← PLists[K-1].CurrEntry.ID + 1
/*
无论当前候选IDX是被接受还是拒绝,在处理完它之后,所有List的指针都需要移动到下一个可能匹配的Cid。这里设定下一个要查找的最小ID是X+1。
*/
31: else
32: /* Skip first K-1 posting lists */
33: NextID ← PLists[K-1].CurrEntry.ID
/*
如果第一个List的当前Cid不等于第K个List的当前Cid,说明前K个List的当前条目没有共同的Cid。此时,我们无法以PLists[K-1]的当前Cid(假设为Y)作为候选,但可以尝试让前K-1个List跳过到Cid Y的位置。
*/
34: for L = 0. . .K-1 do
35: /* Skip to smallest ID such that ID ≥ NextID */
36: PLists[L].SkipTo(NextID)
/*
这是指针跳跃的执行步骤。根据上面计算出的NextID,让前K个(或K-1个)Posting List的指针都跳跃到大于等于NextID的第一个条目上。
SkipTo操作是此算法高效的关键,它避免了逐个遍历无关的条目,实现了“快速前进”。
*/
37: return O用ES可以做吗?
es检索的dsl条件的伪代码如下:
[(不存在性别定向)|| (存在性别定向且满足条件)]
&& [(不存在年龄定向)|| (存在年龄定向且满足条件)]
&& [(不存在标签定向)|| (存在标签定向且满足条件)]
...这样就可以把通投的(无任何定向)广告和有定向且满足条件的广告检索出来。
例如:请求是:26岁的男性用户,那么实际的es的dsl为:
{
"must": [
{
"bool": {
"should": [
{
"bool": {
"must_not": {
"exists": {
"field": "age"
}
}
}
},
{
"bool": {
"should": [
{
"range": {
"age.min": {
"from": null,
"to": 26,
"include_lower": true,
"include_upper": true
}
}
},
{
"range": {
"age.max": {
"from": 26,
"to": null,
"include_lower": true,
"include_upper": true
}
}
}
]
}
}
]
}
},
{
"bool": {
"should": [
{
"bool": {
"must_not": {
"exists": {
"field": "gender"
}
}
}
},
{
"term": {
"gender": "男"
}
}
]
}
}
]
}五、向量索引和图索引
包括暴力(NN),KNN,ANN(近似)
KNN也是暴力搜索的范畴
综述性文章:
https://www.zhihu.com/question/652037964
https://zhuanlan.zhihu.com/p/27399676042
ANN代表一类算法,KNN介于NN和ANN之间:https://www.elastic.co/cn/blog/understanding-ann
- KD树:https://blog.csdn.net/weixin_39910711/article/details/114447104
Annoy是一个以树为数据结构的近似最近邻搜索库,并用在Spotify的推荐系统中。Annoy的核心是不断用选取的两个质心的法平面对空间进行分割,最终将每一个区分的子空间里面的样本数据限制在K以内。对于待插入的样本xi,从根节点依次使用法向量跟xi做内积运算,从而判断使用法平面的哪一边(左子树or右子树)。对于查询向量qi,采用同样的方式(在树结构上体现为从根节点向叶子节点递归遍历),即可定位到跟qi在同一个子空间或者邻近的子空间的样本,这些样本即为qi近邻。为了提高查询的召回,Annoy采用建立多棵树的方式。 - 局部敏感哈希 (LSH):
LSH 是一种强大的 ANN 技术,它会将数据点“哈希”到较低维度空间中,而且在转换过程中能巧妙地保留数据点之间的相似关系。这种聚类方法使得数据点更容易被找到,并且使得 LSH 在搜索庞大的高维数据集(如图像或文本)时在速度和可扩展性方面都能拥有出色表现。而且在提供上述优势的同时,它仍然能够以良好的准确性返回“足够接近的”匹配结果。但请记住,LSH 偶尔也可能产生误报(将非相似点识别为相似),其效果可能会根据距离度量和数据类型而有所不同。有多种旨在处理不同指标(例如欧氏距离、杰卡德相似度)的 LSH 族群,这意味着 LSH 仍然具有很多用途。 - ivf索引,可以就通过https://zhuanlan.zhihu.com/p/27399676042这篇综述来看
- hnsw检索 ( https://yongyuan.name/blog/opq-and-hnsw.html ,
ANN包括的算法:
| 算法类型 | 核心思想 | 代表算法/实现 | 主要特点 | 典型适用场景 |
|---|---|---|---|---|
| 基于空间划分 | 将向量空间划分为多个子区域,搜索时只检查查询点最可能所属的少数几个区域。 | IVF (Inverted File Index)、KD-Tree、Ball-Tree、Annoy(使用随机投影树) | 通过减少需要精确比较的向量数量来提速。KD-Tree在低维效果较好,高维性能下降(维度灾难)。Annoy简单轻量,适合快速原型。 | 低维数据(KD-Tree)、中等规模数据、对内存敏感的场景(IVF系列) |
| 基于图结构 | 构建一个近邻图,查询时通过“导航”图结构(沿着连接邻居的边)逐步靠近目标。 | HNSW(Hierarchical Navigable Small World)、NSG (Navigating Spreading-out Graph) | 查询速度极快,召回率高,是目前性能最好的算法之一。但内存占用较高,构建索引时间较长。 | 高维向量检索(如推荐系统、图像搜索)、对查询速度和精度要求极高的场景 |
| 基于量化 | 将高维向量压缩(编码)成低维度的码字,在压缩空间中进行近似距离计算,显著减少内存占用。 | PQ (Product Quantization)乘积量化、OPQ (Optimized Product Quantization)、SQ (Scalar Quantization) 标量量化 | 内存效率极高,压缩率高。会引入量化误差,精度有一定损失。常与IVF结合形成IVF-PQ等混合方法。 | 海量数据、内存极其敏感、存储成本受限的场景 |
| 基于哈希 | 设计哈希函数使得相似向量更可能被映射到相同的哈希桶中,搜索时只需检查目标桶及邻近桶中的向量。 | LSH (Locality-Sensitive Hashing) | 构建相对简单,对超高维数据有效。但为了达到高召回率通常需要多组哈希表,内存消耗较大,参数调优对性能影响大。 | 高维数据、文本检索、内存尚可、精度要求中等的场景 |
| 混合方法 | 结合多种技术取长补短,例如空间划分的快速过滤+量化的小内存消耗+图索引的高精度导航。 | FAISS (库,支持IVF, PQ, HNSW及组合如IVF-PQ, HNSW+PQ)、Milvus (向量数据库,集成多种索引) | 工业界主流选择,旨在平衡速度、精度和内存使用。 | 大规模生产环境(十亿级以上向量)、需要灵活配置和优化的场景 |
| GPU加速方法 | 利用GPU强大的并行计算能力加速ANN检索过程。 | RAFT (NVIDIA, 含IVF_FLAT, IVF_PQ, Cagra等)、Faiss-GPU | 能实现极快的检索速度(毫秒级响应),尤其适合超大规模数据集和实时性要求极高的场景。但对硬件有要求,受限于GPU显存容量。 | 十亿/万亿级向量的实时检索、高吞吐量场景、追求极致低延迟的应用 |
PQ算法详细解释
lucene,主体是做倒排索引的库,其次还有hnsw算法和标量量化sq算法,也有支持布尔索引
faiss库,主体是做向量索引的库,对上述算法都有实现(ivf、hnsw、lsh、以及对应的pq sq)(常见复合索引PCA+PQ+IVF)
Milvus是向量数据库,也对上述算法都有实现
PS:上述索引如何做增量
